Lnotes

Matrices

In the PreSession Maths course, a matrix was defined as follows:

A matrix is a rectangular array of numbers enclosed in parentheses, conventionally denoted by a capital letter. The number of rows (say [math]m[/math]) and

the number of columns (say [math]n[/math]) determine the order of the matrix ([math]m[/math] [math]\times[/math] [math]n[/math]).

Two examples were given:

[math]\begin{aligned} P & =\left[\begin{array}{rrr} 2 & 3 & 4\\ 3 & 1 & 5 \end{array}\right],\ \ \ Q=\left[\begin{array}{rr} 2 & 3\\ 4 & 3\\ 1 & 5 \end{array}\right],\end{aligned}[/math]

matrices of dimensions [math]2\times3[/math] and [math]3\times2[/math] respectively.

Why study matrices for econometrics? Basically because a data set of several variables, e.g. on the weights and heights of 12 students, can be thought of as a matrix:

[math]\begin{aligned} D & =\left[\begin{array}{cc} 155 & 70\\ 150 & 63\\ 180 & 72\\ 135 & 60\\ 156 & 66\\ 168 & 70\\ 178 & 74\\ 160 & 65\\ 132 & 62\\ 145 & 67\\ 139 & 65\\ 152 & 68 \end{array}\right]\end{aligned}[/math]

The properties of matrices can then be used to facilitate answering all the usual questions of econometrics - list not given here!

Calculations with matrices with explicit numerical elements, as in the examples above is called matrix arithmetic. Matrix algebra is the algebra of matrices where the elements are not made explicit: this is what is really required for econometrics, as we shall see.

As an example of this, a [math]2\times3[/math] matrix might be written as:

[math]\begin{aligned} A & =\left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{array}\right],\end{aligned}[/math]

and would equal [math]P[/math] above if the collection of [math]a_{ij}[/math] were given appropriate numerical values.

A general [math]m\times n[/math] matrix [math]A[/math] can be written as:

[math]\begin{aligned} A & =\left[\begin{array}{rrrr} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right].\end{aligned}[/math]

There is also a typical element notation for matrices:

[math]\begin{aligned} A & =\left\Vert a_{ij}\right\Vert ,\ \ \ \ \ i=1,...,m,j=1,...,n,\end{aligned}[/math]

so that [math]a_{ij}[/math] is the element at the intersection of the [math]i[/math]th row and [math]j[/math]th column in [math]A.[/math]

When [math]m\neq n,[/math] [math]A[/math] is a rectangular matrix; when [math]m=n,[/math] [math]A[/math] is [math]m\times m[/math] or [math]n\times n,[/math] and [math]A[/math] is a square matrix, having the same number of rows or columns.

Rows, columns and vectors

Clearly, there is no reason why [math]m[/math] or [math]n[/math] cannot equal 1: so, an [math]m\times n[/math] matrix with [math]n=1,[/math] i.e. with one column, is usually called a column vector. Similarly, a matrix with one row is a row vector.

There are a lot of advantages to thinking of matrices as collections of row or column vectors, as we shall see. As an example, define the [math]2\times1[/math] column vectors:

[math]\begin{aligned} \mathbf{a} & =\left[\begin{array}{r} 6\\ 3 \end{array}\right]\mathbf{,\ \ \ b}=\left[\begin{array}{r} 2\\ 5 \end{array}\right].\end{aligned}[/math]

and arrange as the columns of the [math]2\times2[/math] matrix

[math]A=\left[\begin{array}{rr} \mathbf{a} & \mathbf{b}\end{array}\right]=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right].\label{eq:axy}[/math]

In general, a column vector [math]\mathbf{x}[/math] with [math]n[/math] elements can be written as:

[math]\begin{aligned} \mathbf{x} & =\left[\begin{array}{c} x_{1}\\ \vdots\\ x_{n} \end{array}\right]\end{aligned}[/math]

What happens when both [math]m[/math] and [math]n[/math] are equal to [math]1?[/math] Then, [math]A[/math] is a [math]1\times1[/math] matrix, but it is also considered to be a real number, or scalar in the language of linear algebra:

[math]\begin{aligned} A & =\left[a_{11}\right]=a_{11}.\end{aligned}[/math]

This is perhaps a little odd, but turns out to be a useful convention in a number of situations.

Transposition of vectors

The rows of the matrix [math]A[/math] in equation (1) can be seen as elements of column vectors, say:

[math]\begin{aligned} \mathbf{c} & =\left[\begin{array}{r} 6\\ 2 \end{array}\right],\ \ \ \boldsymbol{d}=\left[\begin{array}{r} 3\\ 5 \end{array}\right].\end{aligned}[/math]

This representation of row vectors as column vectors is a bit clumsy, so some transformation which converts a column vector into a row vector, and vice versa would be useful. The process of converting a column vector [math]\mathbf{a}[/math] into a row vector is called transposition, and the transposed version of [math]\mathbf{c}[/math] is denoted:

[math]\begin{aligned} \mathbf{c}^{T} & =\left[\begin{array}{rr} 6 & 2\end{array}\right],\end{aligned}[/math]

the [math]^{T}[/math] superscript denoting transposition. In practice, a prime, [math]^{\prime},[/math] is used instead of [math]^{T}.[/math] However, whilst the prime is much simpler to write than the [math]^{T}[/math] sign, it is also much easier to lose track of in writing out long or complicated expressions. So, it is best initially to use [math]^{T}[/math] to denote transposition rather than the prime [math]^{\prime}.[/math]

[math]A[/math] can then be written via its rows as:

[math]\begin{aligned} A & =\left[\begin{array}{r} \mathbf{c}^{T}\\ \boldsymbol{d}^{T} \end{array}\right]=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right].\end{aligned}[/math]

The same ideas can be applied to the matrices [math]P[/math] and [math]Q.[/math]

Operations with matrices

Addition, subtraction and scalar multiplication

For vectors, addition and subtraction are defined only for vectors of the same dimensions. If:

[math]\begin{aligned} \mathbf{x} & =\left[\begin{array}{c} x_{1}\\ \vdots\\ x_{n} \end{array}\right],\,\,\,\,\mathbf{y}=\left[\begin{array}{c} y_{1}\\ \vdots\\ y_{n} \end{array}\right],\\ \mathbf{x+y} & =\left[\begin{array}{c} x_{1}+y_{1}\\ \vdots\\ x_{n}+y_{n} \end{array}\right],\,\,\,\,\mathbf{x-y}=\left[\begin{array}{c} x_{1}-y_{1}\\ \vdots\\ x_{n}-y_{n} \end{array}\right].\end{aligned}[/math]

Clearly, the addition or subtraction operation is elementwise. If [math]\mathbf{x}[/math] and [math]\mathbf{y}[/math] have different dimensions, there will be some elements left over once all the elements of the smaller dimensioned vector have been used up.

Another operation is scalar multiplication: if [math]\lambda[/math] is a real number or scalar, the product [math]\lambda\mathbf{x}[/math] is defined as: [math]\lambda\mathbf{x}=\left[\begin{array}{c} \lambda x_{1}\\ \vdots\\ \lambda x_{n} \end{array}\right],[/math] so that every element of [math]\mathbf{x}[/math] is multiplied by the same scalar [math]\lambda.[/math]

The two types of operation can be combined into the linear combination of vectors [math]\mathbf{x}[/math] and [math]\mathbf{y}[/math]: [math]\lambda\mathbf{x}+\mu\mathbf{y}=\left[\begin{array}{c} \lambda x_{1}\\ \vdots\\ \lambda x_{n} \end{array}\right]+\left[\begin{array}{c} \mu y_{1}\\ \vdots\\ \mu y_{n} \end{array}\right]=\left[\begin{array}{c} \lambda x_{1}+\mu y_{1}\\ \vdots\\ \lambda x_{n}+\mu y_{n} \end{array}\right].[/math] Equally, one can define the linear combination of vectors [math]\mathbf{x,y,}\ldots,\mathbf{z}[/math] by scalars [math]\lambda,\mu,\ldots,\nu[/math] as: [math]\lambda\mathbf{x}+\mu\mathbf{y}+\ldots+\nu\mathbf{z}[/math] with typical element: [math]\lambda x_{i}+\mu y_{i}+\ldots+\nu z_{i},[/math] provided that all the vectors have the same dimension.

For matrices, these ideas carry over immediately: apply to each column of the matrices involved. For example, if [math]A=\left[\begin{array}{rrr} \mathbf{a}_{1} & \ldots & \mathbf{a}_{n}\end{array}\right][/math] and [math]B=\left[\begin{array}{rrr} \mathbf{b}_{1} & \ldots & \mathbf{b}_{n}\end{array}\right],[/math] both [math]m\times n,[/math] then addition and subtraction are defined elementwise, as for vectors:

[math]\begin{aligned} A+B & = & \left[\begin{array}{rrr} \mathbf{a}_{1}+\mathbf{b}_{1} & \ldots & \mathbf{a}_{n}+\mathbf{b}_{n}\end{array}\right]=\left\Vert a_{ij}+b_{ij}\right\Vert ,\\ A-B & = & \left[\begin{array}{rrr} \mathbf{a}_{1}-\mathbf{b}_{1} & \ldots & \mathbf{a}_{n}-\mathbf{b}_{n}\end{array}\right]=\left\Vert a_{ij}-b_{ij}\right\Vert .\end{aligned}[/math]

Scalar multiplication of [math]A[/math] by [math]\lambda[/math] involves multiplying every column vector of [math]A[/math] by [math]\lambda,[/math] and therefore multiplying every element of [math]A[/math] by [math]\lambda[/math]: [math]\lambda A=\left[\begin{array}{rrr} \lambda\mathbf{a}_{1} & \ldots & \lambda\mathbf{a}_{n}\end{array}\right]=\left\Vert \lambda a_{ij}\right\Vert .[/math] With the same idea for [math]B,[/math] the linear combination of [math]A[/math] and [math]B[/math] by [math]\lambda[/math] and [math]\mu[/math] is: [math]\lambda A+\mu B=\left[\begin{array}{rrr} \lambda\mathbf{a}_{1}+\mu\mathbf{b}_{1} & \ldots & \lambda\mathbf{a}_{n}+\mu\mathbf{b}_{n}\end{array}\right]=\left\Vert \lambda a_{ij}+\mu b_{ij}\right\Vert .[/math]

For example, consider the matrices: [math]A=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right],\ \ \ \ \ B=\left[\begin{array}{cc} 1 & 1\\ 1 & -1 \end{array}\right][/math] with [math]\lambda=1,[/math] [math]\mu=-2:[/math] then:

[math]\begin{aligned} \lambda A+\mu B & = & A-2B\\ & = & \left[\begin{array}{cc} 4 & 0\\ 1 & 7 \end{array}\right].\end{aligned}[/math]

Matrix - vector products

Inner product

The simplest form of a matrix vector product is the case where [math]A[/math] consists of one row, so that [math]A[/math] is [math]1\times n[/math]: [math]A=\mathbf{a}^{T}=\left[\begin{array}{rrr} a_{1} & \ldots & a_{n}\end{array}\right].[/math] If [math]\mathbf{x}[/math] is an [math]n\times1[/math] vector: [math]\mathbf{x}=\left[\begin{array}{c} x_{1}\\ \vdots\\ x_{n} \end{array}\right],[/math] the product [math]A\mathbf{x}=\mathbf{a}^{T}\mathbf{x}[/math] is called the inner product and is defined as:

[math]\begin{aligned} \mathbf{a}^{T}\mathbf{x} & =a_{1}x_{1}+\ldots+a_{n}x_{n}.\end{aligned}[/math]

One can see that the definition amounts to multiplying corresponding elements in [math]\mathbf{a}[/math] and [math]\mathbf{x,}[/math] and adding up the resultant products. Writing: [math]\mathbf{a}^{T}\mathbf{x=}\left[\begin{array}{rrr} a_{1} & \ldots & a_{n}\end{array}\right]\left[\begin{array}{c} x_{1}\\ \vdots\\ x_{n} \end{array}\right]=a_{1}x_{1}+\ldots+a_{n}x_{n}[/math] motivates the familiar description of the across and down rule for this product: across and down is the ’multiply corresponding elements’ part of the definition.

Notice that the result of the inner product is a real number, for example: [math]\mathbf{c}^{T}=\left[\begin{array}{rr} 6 & 2\end{array}\right],\ \ \ \mathbf{x}=\left[\begin{array}{r} 6\\ 3 \end{array}\right],\ \ \ \mathbf{c}^{T}\mathbf{x}=\left[\begin{array}{rr} 6 & 2\end{array}\right]\left[\begin{array}{r} 6\\ 3 \end{array}\right]=36+6=42.[/math]

In general, in the product [math]\mathbf{a}^{T}\mathbf{x,}[/math] [math]\mathbf{a}[/math] and [math]\mathbf{x}[/math] must have the same number of elements, [math]n[/math] say, for the product to be defined. If [math]\mathbf{a}[/math] and [math]\mathbf{x}[/math] had different numbers of elements, there would be some elements of [math]\mathbf{a}[/math] or [math]\mathbf{x}[/math] left over or not used in the product: e.g.: [math]\mathbf{b}=\left[\begin{array}{c} 1\\ 2\\ 3 \end{array}\right],\ \ \ \mathbf{x=}\left[\begin{array}{r} 6\\ 3 \end{array}\right].[/math] When the inner product of two vectors is defined, the vectors are said to be conformable.

Orthogonality

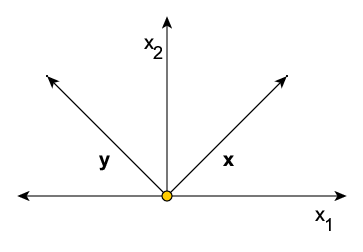
Two vectors [math]\mathbf{x}[/math] and [math]\mathbf{y}[/math] with the property that [math]\mathbf{x}^{T}\mathbf{y}=0[/math] are said to be orthogonal to each other. For example, if: [math]\mathbf{x}=\left[\begin{array}{r} 1\\ 1 \end{array}\right],\ \ \ \mathbf{y}=\left[\begin{array}{r} -1\\ 1 \end{array}\right],[/math] it is clear that [math]\mathbf{x}^{T}\mathbf{y}=0.[/math] This seems a rather innocuous definition, and yet the idea of orthogonality turns out to be extremely important in econometrics.

If [math]\mathbf{x}[/math] and [math]\mathbf{y}[/math] are thought of as points in [math]R^{2},[/math] and arrows are drawn from the origin to [math]\mathbf{x}[/math] and to [math]\mathbf{y,}[/math] then the two arrows are perpendicular to each other - see Figure 1. If [math]\mathbf{y}[/math] were defined as: [math]\mathbf{y}=\left[\begin{array}{r} 1\\ -1 \end{array}\right],[/math] the position of the [math]\mathbf{y}[/math] vector and the corresponding arrow would change, but the perpendicularity property would still hold.

Figure 1

Matrix - vector products

Since the matrix: [math]A=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right][/math] has two rows, now denoted [math]\boldsymbol{\alpha}_{1}^{T}[/math] and [math]\boldsymbol{\alpha}_{2}^{T},[/math] there are two possible inner products with the vector:

[math]\begin{aligned} \mathbf{x} & = & \left[\begin{array}{r} 6\\ 3 \end{array}\right]:\\ \boldsymbol{\alpha}_{1}^{T}\mathbf{x} & = & 42,\ \ \ \ \ \boldsymbol{\alpha}_{2}^{T}\mathbf{x}=33.\end{aligned}[/math]

Assembling the two inner product values into a [math]2\times1[/math] vector defines the product of the matrix [math]A[/math] with the vector [math]\mathbf{x}[/math]: [math]A\mathbf{x}=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]\left[\begin{array}{r} 6\\ 3 \end{array}\right]=\left[\begin{array}{r} \boldsymbol{\alpha}_{1}^{T}\mathbf{x}\\ \boldsymbol{\alpha}_{2}^{T}\mathbf{x} \end{array}\right]=\left[\begin{array}{r} 42\\ 33 \end{array}\right].[/math] Focussing only on the part: [math]\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]\left[\begin{array}{r} 6\\ 3 \end{array}\right]=\left[\begin{array}{r} 42\\ 33 \end{array}\right],[/math] one can see that each element of [math]A\mathbf{x}[/math] is obtained from an across and down argument.

Sometimes this product is described as forming a linear combination of the columns of [math]A[/math] using the scalar elements in [math]\mathbf{x}[/math]: [math]A\mathbf{x}=6\left[\begin{array}{r} 6\\ 3 \end{array}\right]+3\left[\begin{array}{r} 2\\ 5 \end{array}\right].[/math] More generally, if:

[math]\begin{aligned} A & = & \left[\begin{array}{rr} \mathbf{a} & \mathbf{b}\end{array}\right],\ \ \ \ \ \mathbf{x}=\left[\begin{array}{r} \lambda\\ \mu \end{array}\right],\\ A\mathbf{x} & = & \lambda\mathbf{a}+\mu\mathbf{b.}\end{aligned}[/math]

The general version of these ideas for an [math]m\times n[/math] matrix [math]A[/math]: [math]A=\left[\begin{array}{rrrr} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right]=\left[\begin{array}{rrrr} \mathbf{a}_{1} & \mathbf{a}_{2} & \ldots & \mathbf{a}_{n}\end{array}\right].[/math] is straightforward. If [math]\mathbf{x}[/math] is an [math]n\times1[/math] vector, then the vector [math]A\mathbf{x}[/math] is, by the across and down rule:

[math]A\mathbf{x}=\left[\begin{array}{rrrr} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ \vdots\\ x_{n} \end{array}\right]=\left[\begin{array}{c} a_{11}x_{1}+\ldots+a_{1n}x_{n}\\ a_{21}x_{1}+\ldots+a_{2n}x_{n}\\ \vdots\\ a_{m1}x_{1}+\ldots+a_{mn}x_{n} \end{array}\right]=\left[\begin{array}{c} \sum\limits _{j=1}^{n}a_{1j}x_{j}\\ \sum\limits _{j=1}^{n}a_{2j}x_{j}\\ \vdots\\ \sum\limits _{j=1}^{n}a_{mj}x_{j} \end{array}\right],\label{eq:ab}[/math]

so that the typical element, the [math]i[/math]th, is [math]\sum\limits _{j=1}^{n}a_{ij}x_{j}.[/math] Equally, [math]A\mathbf{x}[/math] is the linear combination [math]\mathbf{a}_{1}x_{1}+\ldots+\mathbf{a}_{n}x_{n}[/math] of the columns of [math]A.[/math]

Matrix - matrix products

Suppose that [math]A[/math] is [math]m\times n,[/math] with columns [math]\mathbf{a}_{1},\ldots,\mathbf{a}_{n},[/math] and [math]B[/math] is [math]n\times r,[/math] with columns [math]\mathbf{b}_{1},\ldots,\mathbf{b}_{r}.[/math] Clearly, each product [math]A\mathbf{b}_{1},...,A\mathbf{b}_{r}[/math] exists, and is [math]m\times1.[/math] These products can be arranged as the columns of a matrix as [math]\left[\begin{array}{rrrr} A\mathbf{b}_{1} & A\mathbf{b}_{2} & \ldots & A\mathbf{b}_{r}\end{array}\right][/math] and this matrix is defined to be the product [math]C[/math] of the matrices [math]A[/math] and [math]B[/math]: [math]C=\left[\begin{array}{rrrr} A\mathbf{b}_{1} & A\mathbf{b}_{2} & \ldots & A\mathbf{b}_{r}\end{array}\right]=AB.[/math] By construction, this must be an [math]m\times r[/math] matrix, since each column is [math]m\times1[/math] and there are [math]r[/math] columns.

This is not the usual presentation of the definition of the product of two matrices, which relies on the across and down rule mentioned earlier, and focusses on the elements of each matrix [math]A[/math] and [math]B.[/math] Set:

[math]\begin{aligned} B & = & \left[\begin{array}{rrrr} \mathbf{b}_{1} & \mathbf{b}_{2} & \ldots & \mathbf{b}_{r}\end{array}\right]\ \ \ \ \ \ \ \text{(by columns)}\\ & = & \left\Vert b_{ik}\right\Vert ,\ \ \ \ \ i=1,...,n,k=1,...,r\ \ \ \ \ \ \ \text{(typical element)}\\ & = & \left[\begin{array}{rrrr} b_{11} & b_{12} & \ldots & b_{1r}\\ b_{21} & b_{22} & \ldots & b_{2r}\\ \vdots & \vdots & \ddots & \vdots\\ b_{n1} & b_{n2} & \ldots & b_{nr} \end{array}\right]\ \ \ \ \ \ \ \text{(the array)}\end{aligned}[/math]

What does the typical element of the [math]m\times r[/math] matrix [math]C[/math] look like? Start with the [math]k[/math]th column of [math]C,[/math] which is [math]A\mathbf{b}_{k}.[/math] The [math]i[/math]th element in [math]A\mathbf{b}_{k}[/math] is, from equation (2), the inner product of the elements of the [math]i[/math]th row in [math]A[/math]: [math]\left[\begin{array}{rrrr} a_{i1} & a_{i2} & \ldots & a_{in}\end{array}\right],[/math] with the elements of [math]\mathbf{b}_{k},[/math] so that the inner product is: [math]a_{i1}b_{1k}+a_{i2}b_{2k}+\ldots+a_{in}b_{nk}=\sum_{j=1}^{n}a_{ij}b_{jk}.[/math]

So, the [math]ik[/math]th element of [math]C[/math] is: [math]c_{ik}=a_{i1}b_{1k}+a_{i2}b_{2k}+\ldots+a_{in}b_{nk}=\sum_{j=1}^{n}a_{ij}b_{jk}.[/math] We can see this arising from an across and down calculation by writing:

[math]\begin{aligned} C & = & AB\label{eq:c_ab}\\ & = & \left[\begin{array}{rrrr} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & \ldots & a_{2n}\\ \vdots & \vdots & & \vdots\\ a_{i1} & a_{i2} & \ldots & a_{in}\\ \vdots & \vdots & & \vdots\\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right]\left[\begin{array}{rrrrrr} b_{11} & b_{12} & \ldots & b_{1k} & \ldots & b_{1r}\\ b_{21} & b_{22} & \ldots & b_{2k} & \ldots & b_{2r}\\ \vdots & \vdots & & \vdots & & \vdots\\ b_{n1} & b_{n2} & \ldots & b_{nk} & \ldots & b_{nr} \end{array}\right]\\ & = & \left\Vert \sum_{j=1}^{n}a_{ij}b_{jk}\right\Vert .\end{aligned}[/math]

These ideas are simple, but a little tedious. Numerical examples are equally tedious! As an example, using: [math]A=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right],[/math] we can find the matrix [math]B[/math] such that

1. the first column of [math]AB[/math] adds together the columns of [math]A,[/math]
2. the second column is the difference of the first and second columns of [math]A,[/math]
3. the third column is [math]2\times[/math] the first column of [math]A,[/math]
4. the fourth column is zero.

It is easy to check that [math]B[/math] is: [math]B=\left[\begin{array}{rrrr} 1 & 1 & 2 & 0\\ 1 & -1 & 0 & 0 \end{array}\right][/math] and that:

[math]\begin{aligned} C & = & AB\\ & = & \left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]\left[\begin{array}{rrrr} 1 & 1 & 2 & 0\\ 1 & -1 & 0 & 0 \end{array}\right]\\ & = & \left[\begin{array}{cccc} 8 & 4 & 12 & 0\\ 8 & -2 & 6 & 0 \end{array}\right].\end{aligned}[/math]

Arithmetic calculations of matrix products almost always use the elementwise across and down formula. However, there are many situations in econometrics where algebraic rather than arithmetic arguments are required. In these cases, the viewpoint of matrix multiplication as linear combinations of columns is much more powerful.

Clearly one can give many more examples of different dimensions and complexities - but the same basic rules apply. To multiply two matrices [math]A[/math] and [math]B[/math] together, the number of columns in [math]A[/math] must match the number of rows in [math]B[/math] - this is conformability in action again. The resulting product will have number of rows equal to the number in [math]A[/math] and number of columns equal to the number in [math]B.[/math]

If this conformability rule does not hold, then the product of [math]A[/math] and [math]B[/math] is not defined.

Matlab

One should also say that as the dimensions of the matrices increases, so the tediousness of the calculations increase. The solution to this for numerical calculation is to appeal to the computer. Programs like Matlab and Excel (and a number of others, some of them free) resolve this difficulty easily.

In Matlab, symbols for row or column vectors do not need any particular differentiation: they are distinguished by how they are defined. For example, the following Matlab commands define rowvec as a [math]1\times4[/math] vector, and colvec as a [math]4\times1[/math] vector, then display the contents of these variables, and do a calculation:

>> rowvec = [1 2 3 4]; 

>> colvec = [1;2;3;4]; 

>> rowvec

rowvec =

1 2 3 4

>> colvec

colvec =

1 2 3 4 

>> rowvec*colvec

ans =

30 

So, the semi-colon indicates the end of a row in a matrix or vector; it can be replaced by a carriage return. Notice the difference in how a row vector and a column vector is defined. One can see that the product rowvec*colvec is well defined, just because rowvec is a [math]1\times4[/math] vector, and colvec is a [math]4\times1[/math] vector.

Matlab also allows elementwise multiplication of two vectors using the [math]\centerdot\ast[/math] operator: if: [math]\mathbf{x}=\left[\begin{array}{r} x_{1}\\ x_{2} \end{array}\right],\ \ \ \mathbf{y}=\left[\begin{array}{r} y_{1}\\ y_{2} \end{array}\right],[/math] then: [math]\mathbf{x}\centerdot\ast\mathbf{y}=\left[\begin{array}{r} x_{1}y_{1}\\ x_{2}y_{2} \end{array}\right][/math] and one can see that the inner product of [math]\mathbf{x}[/math] and [math]\mathbf{y}[/math] can be obtained as the sum of the elements of [math]\mathbf{x}[/math] and [math]\mathbf{y.}[/math] In Matlab, this would be obtained as: [math]\text{sum}\left(\mathbf{x}\centerdot\ast\mathbf{y}\right).[/math]

In the example above, this calculation fails since rowvec is a [math]1\times4[/math] vector, and colvec is a [math]4\times1[/math] vector:

>> sum(rowvec .* colvec) ??? 

Error using ==> times Matrix dimensions must agree. 

For this to work, rowvec would have to be transposed as rowvec’, so that transposition in Matlab is very natural.

Allowing for such difficulties, matrix multiplication in Matlab is very simple:

>> A = [6 2; 3 5];

>> B = [1 1 2 0;1 -1 0 0];

>> C = A * B; 

>> disp(C)

 8 4 1

 2 0 8 

-2 6 0 

Notice how the matrices are defined here through their rows. The disp() command displays the contents of the object referred to.

It is less natural in Matlab to define matrices by columns - a typical example of how mathematics and computing have conflicts of notation. However, once columns [math]\mathbf{a}[/math] and [math]\mathbf{b}[/math] have been defined, the concatenation operation [math]\left[\begin{array}{rr} \mathbf{a} & \mathbf{b}\end{array}\right][/math] collects the columns into a matrix:

>> a = [6;2]; 

>> b = [3;5]; 

>> C = [a b]; 

>> disp(C)

6 3 

2 5 

Notice that the disp(C) command does not label the result that is printed out. Simply typing C would preface the output by C =.

Pre and Post Multiplication

If [math]C=AB,[/math] as above, say that [math]B[/math] is pre-multiplied by [math]A[/math] to get [math]C,[/math] and that [math]A[/math] is post-multiplied by [math]B[/math] to get [math]C.[/math]

This distinction between pre and post multiplication is important, in the following sense. Suppose that [math]A[/math] and [math]B[/math] are matrices such that the products [math]AB[/math] and [math]BA[/math] are both defined. If [math]A[/math] is [math]m\times n,[/math] [math]B[/math] must have [math]n[/math] rows for [math]AB[/math] to be defined. For [math]BA[/math] to be defined, [math]B[/math] must have [math]m[/math] columns to match the [math]m[/math] rows in [math]A.[/math] So, [math]AB[/math] and [math]BA[/math] are both defined if [math]A[/math] is [math]m\times n[/math] and [math]B[/math] is [math]n\times m.[/math]

Even when both products are defined, there is no reason for the two products coincide. The first thing to notice is that [math]AB[/math] is a square, [math]m\times m,[/math] matrix, whilst [math]BA[/math] is a square, [math]n\times n,[/math] matrix. Different sized matrices cannot be equal. To illustrate, use the matrices: [math]B_{2}=\left[\begin{array}{rr} 6 & -3\\ 2 & 5\\ -3 & 1 \end{array}\right],\ \ \ C=\left[\begin{array}{rrr} 6 & 2 & -3\\ 3 & 5 & -1 \end{array}\right]:[/math]

[math]\begin{aligned} B_{2}C & = & \left[\begin{array}{rr} 6 & -3\\ 2 & 5\\ -3 & 1 \end{array}\right]\left[\begin{array}{rrr} 6 & 2 & -3\\ 3 & 5 & -1 \end{array}\right]=\left[\begin{array}{rrr} 27 & -3 & -15\\ 27 & 29 & -11\\ -15 & -1 & 8 \end{array}\right],\\ CB_{2} & = & \left[\begin{array}{rrr} 6 & 2 & -3\\ 3 & 5 & -1 \end{array}\right]\left[\begin{array}{rr} 6 & -3\\ 2 & 5\\ -3 & 1 \end{array}\right]=\left[\begin{array}{cc} 49 & -11\\ 31 & 15 \end{array}\right].\end{aligned}[/math]

Even when [math]m=n,[/math] so that [math]AB[/math] and [math]BA[/math] are both [math]m\times m[/math] matrices, the products can differ: for example:

[math]\begin{aligned} A & = & \left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right],\ \ \ B=\left[\begin{array}{cc} 1 & 1\\ 1 & -1 \end{array}\right],\\ AB & = & \left[\begin{array}{cc} 8 & 4\\ 8 & -2 \end{array}\right],\ \ \ \ \ BA=\left[\begin{array}{cc} 9 & 7\\ 3 & -3 \end{array}\right].\end{aligned}[/math]

In cases where [math]AB=BA,[/math] the matrices [math]A[/math] and [math]B[/math] are said to commute.

Transposition

A column vector [math]\mathbf{x}[/math] can be converted to a row vector [math]\mathbf{x}^{T}[/math] by transposition: [math]\mathbf{x}=\left[\begin{array}{c} x_{1}\\ \vdots\\ x_{n} \end{array}\right],\ \ \ \ \ \mathbf{x}^{T}=\left[\begin{array}{rrr} x_{1} & \ldots & x_{n}\end{array}\right].[/math] Transposing [math]\mathbf{x}^{T}[/math] as [math]\left(\mathbf{x}^{T}\right)^{T}[/math] reproduces the original vector [math]\mathbf{x.}[/math] How do these ideas carry over to matrices?

If the [math]m\times n[/math] matrix [math]A[/math] can be written as [math]A=\left[\begin{array}{rrr} \mathbf{a}_{1} & \ldots & \mathbf{a}_{n}\end{array}\right],[/math] the transpose of [math]A,[/math] [math]A^{T},[/math] is defined as the matrix whose rows are [math]\mathbf{a}_{i}^{T}[/math]: [math]A^{T}=\left[\begin{array}{c} \mathbf{a}_{1}^{T}\\ \vdots\\ \mathbf{a}_{n}^{T} \end{array}\right].[/math] In terms of elements, if: [math]\mathbf{a}_{i}=\left[\begin{array}{c} a_{1i}\\ \vdots\\ a_{ni} \end{array}\right][/math] then: [math]A=\left[\begin{array}{rrrr} a_{11} & a_{12} & \ldots & a_{1n}\\ \vdots & \vdots & & \vdots\\ a_{i1} & a_{i2} & \ldots & a_{in}\\ \vdots & \vdots & & \vdots\\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right],\ \ \ \ \ A^{T}=\left[\begin{array}{rrrrr} a_{11} & \ldots & a_{i1} & \ldots & a_{m1}\\ a_{12} & \ldots & a_{i2} & \ldots & a_{m2}\\ \vdots & & \vdots & & \vdots\\ a_{1n} & \ldots & a_{in} & \ldots & a_{mn} \end{array}\right].[/math] One can see that the first column of [math]A[/math] has now become the first row of [math]A^{T}.[/math] Notice too that [math]A^{T}[/math] is an [math]n\times m[/math] matrix if [math]A[/math] is an [math]m\times n[/math] matrix.

Transposing [math]A^{T}[/math] takes the first column of [math]A^{T}[/math] and writes it as a row, which coincides with the first row of [math]A.[/math] The same argument applies to the other columns of [math]A^{T},[/math] so that [math]\left(A^{T}\right)^{T}=A.[/math]

The product rule for transposition

This states that if [math]C=AB,[/math] then [math]C^{T}=B^{T}A^{T}.[/math]

How to see this? Consider the following example: [math]A=\left[\begin{array}{rrr} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \end{array}\right],\ \ \ B=\left[\begin{array}{rrrr} b_{11} & b_{12} & b_{13} & b_{14}\\ b_{21} & b_{22} & b_{23} & b_{24}\\ b_{31} & b_{32} & b_{33} & b_{34} \end{array}\right][/math] where:

[math]c_{23}=a_{21}b_{13}+a_{22}b_{23}+a_{23}b_{33}=\sum_{k=1}^{3}a_{2k}b_{k3}.\label{eq:c23}[/math]

One can see that: [math]B^{T}A^{T}=\left[\begin{array}{rrr} b_{11} & b_{21} & b_{31}\\ b_{12} & b_{22} & b_{32}\\ b_{13} & b_{23} & b_{33}\\ b_{14} & b_{24} & b_{34} \end{array}\right]\left[\begin{array}{rr} a_{11} & a_{21}\\ a_{12} & a_{22}\\ a_{13} & a_{23} \end{array}\right][/math] and that the [math]\left(3,2\right)[/math] element of this product is actually [math]c_{23}[/math]: [math]b_{13}a_{21}+b_{23}a_{22}+b_{33}a_{23}=a_{21}b_{13}+a_{22}b_{23}+a_{23}b_{33}=c_{23}.[/math] In summation notation, we see that from [math]B^{T}A^{T}[/math]: [math]c_{23}=\sum_{k=1}^{3}b_{k3}a_{2k},[/math] where the position of the index of summation is due to the transposition. So, in summation notation, the calculation of [math]c_{23}[/math] from [math]B^{T}A^{T}[/math] equals that from equation (4).

More generally, the [math]\left(i,j\right)[/math] element of [math]AB[/math]: [math]\sum_{k=1}^{3}a_{ik}b_{kj}[/math] is the [math]\left(j,i\right)[/math] element of [math]B^{T}A^{T}.[/math] But this means that [math]B^{T}A^{T}[/math] must be the transpose of [math]AB,[/math] since the elements in the [math]i[/math]th row of [math]AB[/math] are being written in the [math]i[/math]th column of [math]B^{T}A^{T}.[/math]

This Product Rule for Transposition can be applied again to find the transpose [math]\left(C^{T}\right)^{T}[/math] of [math]C^{T}[/math]: [math]\left(C^{T}\right)^{T}=\left(B^{T}A^{T}\right)^{T}=\left(A^{T}\right)^{T}\left(B^{T}\right)^{T}=AB=C.[/math]

Special Types of Matrix

The zero matrix

The most obvious special type of matrix is one whose elements are all zeros. In typical element notation, the zero matrix is: [math]0=\left\Vert 0\right\Vert .[/math] Since there is no indexing on the elements, it is not obvious what the dimension of this matrix is, Sometimes one writes [math]0_{mn}[/math] to indicate a zero matrix of dimension [math]m\times n.[/math] The same ideas apply to vectors whose elements are all zero.

The effect of the zero matrix in any product that is defined is simple: [math]0A=0,\ \ \ \ \ B0=0.[/math] This is easy to check using the across and down rule.

The identity or unit matrix

Vectors of the form:

[math]\begin{aligned} \left[\begin{array}{r} 1\\ 0 \end{array}\right],\left[\begin{array}{r} 0\\ 1 \end{array}\right]\ \ \ \ \ \text{in }2\ \text{dimensions}\\ \left[\begin{array}{c} 1\\ 0\\ 0 \end{array}\right],\left[\begin{array}{c} 0\\ 1\\ 0 \end{array}\right],\left[\begin{array}{c} 0\\ 0\\ 1 \end{array}\right]\ \ \ \ \ \text{in }3\ \text{dimensions}\\ \left[\begin{array}{r} 1\\ 0\\ \vdots\\ 0\\ 0 \end{array}\right],\left[\begin{array}{r} 0\\ 1\\ 0\\ \vdots\\ 0 \end{array}\right],\ldots,\left[\begin{array}{r} 0\\ 0\\ \vdots\\ 0\\ 1 \end{array}\right]\ \ \ \ \ \text{in }n\ \text{dimensions}\end{aligned}[/math]

are called coordinate vectors. They are often given a characteristic notation, [math]\mathbf{e}_{1},\ldots,\mathbf{e}_{n},[/math] in [math]n[/math] dimensions. When arranged as columns of a matrix in the natural order, [math]\mathbf{e}_{1},\ldots,\mathbf{e}_{n},[/math] a matrix with a characteristic pattern elements emerges, with a special notation:

[math]\begin{aligned} \left[\begin{array}{rr} \mathbf{e}_{1} & \mathbf{e}_{2}\end{array}\right] & = & \left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]=I_{2}\\ \left[\begin{array}{rrr} \mathbf{e}_{1} & \mathbf{e}_{2} & \mathbf{e}_{3}\end{array}\right] & = & \left[\begin{array}{rrr} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]=I_{3}\\ \left[\begin{array}{rrrr} \mathbf{e}_{1} & \mathbf{e}_{2} & \ldots & \mathbf{e}_{n}\end{array}\right] & = & \left[\begin{array}{rrrr} 1 & 0 & \ldots & 0\\ 0 & 1 & \ldots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \ldots & 1 \end{array}\right]=I_{n}.\end{aligned}[/math]

The diagonal of this matrix is where the 1 elements are located, and every other element is zero.

Consider the effect of [math]I_{2}[/math] on the matrix: [math]A=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right][/math] by both pre and post multiplication:

[math]\begin{aligned} I_{2}A & = & \left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]=A,\\ AI_{2} & = & \left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]=\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]=A,\end{aligned}[/math]

as is easily checked by the across and down rule.

Because any matrix is left unchanged by pre or post multiplication by an appropriately dimensioned [math]I_{n},[/math] [math]I_{n}[/math] is called an identity matrix of dimension [math]n.[/math] Sometimes it is called a unit matrix of dimension [math]n.[/math] Notice that [math]I_{n}[/math] is necessarily a square matrix.

Diagonal matrices

The identity matrix is an example of a diagonal matrix, a matrix whose elements are all zero except for those on the diagonal. Usually diagonal matrices are taken to be square, for example: [math]D=\left[\begin{array}{rrr} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3 \end{array}\right].[/math] They also produce characteristic effects when pre or post multiplying another matrix.

Consider the diagonal matrix: [math]B=\left[\begin{array}{cc} 2 & 0\\ 0 & -2 \end{array}\right][/math] and the products [math]AB,[/math] [math]BA[/math] for [math]A[/math] as defined in the previous section:

[math]\begin{aligned} AB & = & \left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]\left[\begin{array}{cc} 2 & 0\\ 0 & -2 \end{array}\right]=\left[\begin{array}{cc} 12 & -4\\ 6 & -10 \end{array}\right],\\ BA & = & \left[\begin{array}{cc} 2 & 0\\ 0 & -2 \end{array}\right]\left[\begin{array}{cc} 6 & 2\\ 3 & 5 \end{array}\right]=\left[\begin{array}{cc} 12 & 4\\ -6 & -10 \end{array}\right].\end{aligned}[/math]

Comparing the results, we can deduce that post multiplication by a diagonal matrix multiplies each column of [math]A[/math] by the corresponding diagonal element, whereas pre multiplication multiplies each row by the corresponding diagonal element.

Symmetric matrices

Symmetric matrices are matrices having the property that [math]A=A^{T}.[/math] Notice that such matrices must be square, since if [math]A[/math] is [math]m\times n,[/math] [math]A^{T}[/math] is [math]n\times m,[/math] and to have equality of [math]A[/math] and [math]A^{T},[/math] they must have the same dimension, so that [math]m=n[/math] is required.

Suppose that [math]A[/math] is a [math]3\times3[/math] symmetric matrix, with typical element [math]a_{ij}[/math]: [math]A=\left[\begin{array}{rrr} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right],[/math] so that: [math]A^{T}=\left[\begin{array}{rrr} a_{11} & a_{21} & a_{31}\\ a_{12} & a_{22} & a_{32}\\ a_{13} & a_{23} & a_{33} \end{array}\right].[/math] Equality of matrices is defined as equality of all elements. This is fine on the diagonals, since [math]A[/math] and [math]A^{T}[/math] have the same diagonal elements. For the off diagonal elements, we end up with the requirements: [math]a_{12}=a_{21},\ \ \ a_{13}=a_{31},\ \ \ a_{23}=a_{32}[/math] or more generally: [math]a_{ij}=a_{ji}\ \ \ \ \ \text{for}\ i\neq j.[/math]

The effect of this conclusion is that in a symmetric matrix, the ’triangle’ of above diagonal elements coincides with the triangle of below diagonal elements. It is as if the upper triangle is folded over the diagonal to become the lower triangle.

A simple example is: [math]A=\left[\begin{array}{cc} 1 & 2\\ 2 & 1 \end{array}\right].[/math] A more complicated example uses the [math]2\times3[/math] matrix [math]C[/math]: [math]C=\left[\begin{array}{rrr} 6 & 2 & -3\\ 3 & 5 & -1 \end{array}\right][/math] and calculates the [math]3\times3[/math] matrix:

[math]\begin{aligned} C^{T}C & = & \left[\begin{array}{cc} 6 & 3\\ 2 & 5\\ -3 & -1 \end{array}\right]\left[\begin{array}{rrr} 6 & 2 & -3\\ 3 & 5 & -1 \end{array}\right]\\ & = & \left[\begin{array}{rrr} 45 & 27 & -21\\ 27 & 29 & -11\\ -21 & -11 & 10 \end{array}\right],\end{aligned}[/math]

which is clearly symmetric.

This illustrates the general proposition that if [math]A[/math] is an [math]m\times n[/math] matrix, the product [math]A^{T}A[/math] is a symmetric [math]n\times n[/math] matrix. Proof? Compute the transpose of [math]A^{T}A[/math] using the product rule for transposition: [math]\left(A^{T}A\right)^{T}=A^{T}\left(A^{T}\right)^{T}=A^{T}A.[/math] Since [math]A^{T}A[/math] is equal to its transpose, it must be a symmetric matrix. Such symmetric matrices appear frequently in econometrics.

It should be clear that diagonal matrices are symmetric, since all their off-diagonal elements are equal (zero), and thence the identity matrix [math]I_{n}[/math] is also symmetric.

The outer product

The inner product of two [math]n\times1[/math] vectors [math]\mathbf{x}[/math] and [math]\mathbf{y}[/math], [math]\mathbf{x}^{T}\mathbf{y}[/math], is automatically a [math]1\times1[/math] quantity, a scalar, although it can be interpreted as a [math]1\times1[/math] matrix, a matrix with a single element.

Suppose one considered the product of [math]\mathbf{x}[/math] with [math]\mathbf{x}^{T}.[/math] Is this defined? If [math]A[/math] is [math]m\times n[/math] and [math]B[/math] is [math]n\times r,[/math] then the product [math]AB[/math] is [math]m\times r.[/math] Applying this logic to [math]\mathbf{xx}^{T},[/math] this is [math]\left(n\times1\right)\left(1\times n\right),[/math] so the resulting product is defined, and is an [math]n\times n[/math] matrix - the outer product of [math]\mathbf{x}[/math] and [math]\mathbf{x}^{T},[/math] the word ’outer’ being used to distinguish from the inner product.

How does the across and down rule work here? Suppose that: [math]\mathbf{x}=\left[\begin{array}{r} 6\\ 3 \end{array}\right].[/math] Then: [math]\mathbf{xx}^{T}=\left[\begin{array}{r} 6\\ 3 \end{array}\right]\left[\begin{array}{rr} 6 & 3\end{array}\right].[/math] Here, there is [math]1[/math] element in row one of the ’matrix’ [math]\mathbf{x,}[/math] and [math]1[/math] element in column one of the matrix [math]\mathbf{x}^{T},[/math] so the across and down rule still works - it is just that there is only one product per row and column combination. So: [math]\mathbf{xx}^{T}=\left[\begin{array}{cc} 36 & 18\\ 18 & 9 \end{array}\right],[/math] and it is obvious from this that [math]\mathbf{xx}^{T}[/math] is a symmetric matrix.

One can see that this outer product need not be restricted to vectors of the same dimension. If [math]\mathbf{x}[/math] is [math]n\times1[/math] and [math]\mathbf{y}[/math] is [math]m\times1,[/math] then: [math]\mathbf{xy}^{T}=\left[\begin{array}{c} x_{1}\\ \vdots\\ x_{n} \end{array}\right]\left[\begin{array}{rrr} y_{1} & \ldots & y_{m}\end{array}\right]=\left[\begin{array}{rrrr} x_{1}y_{1} & x_{1}y_{2} & \ldots & x_{1}y_{m}\\ x_{2}y_{1} & x_{2}y_{2} & \ldots & x_{2}y_{m}\\ \\ x_{n}y_{1} & x_{n}y_{2} & \ldots & x_{n}y_{m} \end{array}\right].[/math] So, [math]\mathbf{xy}^{T}[/math] is [math]n\times m,[/math] and consists of rows which are [math]\mathbf{y}^{T}[/math] multiplied by an element of the [math]\mathbf{x}[/math] vector.

Another interesting and useful example involves a vector with every element equal to [math]1[/math]: [math]\mathbf{1}=\left[\begin{array}{c} 1\\ \vdots\\ 1 \end{array}\right].[/math] Sometimes this is written as [math]\mathbf{1}_{n}[/math] to indicate an [math]n\times1[/math] vector, and is called the sum vector. Why? Consider the impact of [math]\mathbf{1}_{2}[/math] on the [math]2\times1[/math] vector [math]\mathbf{x}[/math] used above: [math]\mathbf{1}_{2}^{T}\mathbf{x}=\left[\begin{array}{rr} 1 & 1\end{array}\right]\left[\begin{array}{r} 6\\ 3 \end{array}\right]=9,[/math] i.e. an inner product of [math]\mathbf{x}[/math] with the sum vector is the sum of the elements of [math]\mathbf{x.}[/math] Dividing through by the number of elements in [math]\mathbf{x}[/math] produces the average of the elements of [math]\mathbf{x}[/math] - i.e. the ’sample mean’ of the elements of [math]\mathbf{x.}[/math]

The outer product of [math]\mathbf{x}[/math] with [math]\mathbf{1}_{2}[/math] is also interesting:

[math]\begin{aligned} \mathbf{1}_{2}\mathbf{x}^{T} & = & \left[\begin{array}{r} 1\\ 1 \end{array}\right]\left[\begin{array}{rr} 6 & 3\end{array}\right]=\left[\begin{array}{cc} 6 & 3\\ 6 & 3 \end{array}\right],\\ \mathbf{x1}_{2}^{T} & = & \left[\begin{array}{r} 6\\ 3 \end{array}\right]\left[\begin{array}{rr} 1 & 1\end{array}\right]=\left[\begin{array}{cc} 6 & 6\\ 3 & 3 \end{array}\right],\end{aligned}[/math]

showing that pre multiplication of an [math]\mathbf{x}^{T}[/math] by [math]\mathbf{1}[/math] repeats [math]\mathbf{x}^{T}[/math] as rows of the product, whilst post multiplication of [math]\mathbf{x}[/math] by [math]\mathbf{1}^{T}[/math] repeats [math]\mathbf{x}[/math] as the columns of the product.

Finally: [math]\mathbf{1}_{n}\mathbf{1}_{n}^{T}=\left[\begin{array}{rrr} 1 & \ldots & 1\\ 1 & \ldots & 1\\ 1 & \ldots & 1 \end{array}\right],[/math] an [math]n\times n[/math] matrix with every element equal to [math]1.[/math] This type of matrix also appears in econometrics!

Triangular matrices

A square lower triangular matrix has all elements above the main diagonal equal to zero, whilst a square upper triangular matrix has all elements below the main diagonal equal to zero. A simple example of a lower triangular matrix is: [math]A=\left[\begin{array}{rrr} a_{11} & 0 & 0\\ a_{21} & a_{22} & 0\\ a_{31} & a_{32} & a_{33} \end{array}\right].[/math] Clearly, for this matrix, [math]A^{T}[/math] is an upper triangular matrix.

One can adapt the definition to rectangular matrices: for example, if two arbitrary rows are added to [math]A,[/math] so that it becomes [math]5\times3,[/math] it would still be considered lower triangular. Equally, if, for example, the third column of [math]A[/math] above is removed, [math]A[/math] is still considered lower triangular.

Often, we use unit triangular matrices, where the diagonal elements are all equal to [math]1:[/math] e.g.:

[math]\left[\begin{array}{rrr} 1 & 2 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1 \end{array}\right].\label{eq:lt_matrix}[/math]

Partitioned matrices

Sometimes, especially with big matrices, it is useful to organise the elements of the matrix into components which are themselves matrices, for example: [math]B=\left[\begin{array}{rrrr} 1 & 2 & 0 & 0\\ 8 & 3 & 0 & 0\\ 0 & 0 & 7 & 4\\ 0 & 0 & 6 & 5 \end{array}\right][/math] Here it would be reasonable to write: [math]B=\left[\begin{array}{cc} B_{11} & 0\\ 0 & B_{22} \end{array}\right],[/math] where [math]B_{ii},i=1,2,[/math] represent [math]2\times2[/math] matrices. [math]B[/math] is an example of a partitioned matrix: that is, an [math]m\times n[/math] matrix [math]A[/math] say: [math]A=\left\Vert a_{ij}\right\Vert ,[/math] where the elements of [math]A[/math] are organised into sub-matrices. An example might be:

[math]A=\left[\begin{array}{rrr} A_{11} & A_{12} & A_{23}\\ A_{21} & A_{22} & A_{23} \end{array}\right],\label{eq:partition_a}[/math]

where the sub - matrices in the first row block have [math]r[/math] rows, and therefore [math]m-r[/math] rows in the second row block. The column blocks might be defined by (for example) 3 columns in the first column block, 4 in the second and [math]n-7[/math] in the third column block.

Another simple example might be: [math]A=\left[\begin{array}{rrr} A_{1} & A_{2} & A_{3}\end{array}\right],\ \ \ \ \ \mathbf{x=}\left[\begin{array}{c} \mathbf{x}_{1}\\ \mathbf{x}_{2}\\ \mathbf{x}_{3} \end{array}\right],[/math] where [math]A[/math] and therefore [math]A_{1},A_{2},A_{3}[/math] have [math]m[/math] rows, [math]A_{1}[/math] has [math]n_{1}[/math] columns, [math]A_{2}[/math] has [math]n_{2}[/math] columns, [math]A_{3}[/math] has [math]n_{3}[/math] columns. The subvectors in [math]\mathbf{x}[/math] must have [math]n_{1},n_{2}[/math] and [math]n_{3}[/math] rows respectively, for the product [math]A\mathbf{x}[/math] to exist.

Suppose that [math]n_{1}+n_{2}+n_{3}=n,[/math] so that [math]A[/math] is [math]m\times n.[/math] The [math]i[/math]th element of [math]A\mathbf{x}[/math] is: [math]\sum_{i=1}^{n}a_{ij}x_{j}[/math] but the summation can be broken up into the first [math]n_{1}[/math] terms: [math]\sum_{i=1}^{n_{1}}a_{ij}x_{j},[/math] the next [math]n_{2}[/math] terms: [math]\sum_{i=n_{1}+1}^{n_{1}+n_{2}}a_{ij}x_{j},[/math] and the next [math]n_{3}[/math] terms; [math]\sum_{i=n_{1}+n_{2}+1}^{n}a_{ij}x_{j}.[/math]

The point about the use of partitioned matrices is that the product [math]A\mathbf{x}[/math] can be represented as: [math]A\mathbf{x}=A_{1}\mathbf{x}_{1}+A_{2}\mathbf{x}_{2}+A\mathbf{x}_{3}[/math] by applying the across and down rule to the submatrices and the subvectors, a much simpler representation than the use of summations.

Each of the components is a conformable matrix-vector product: this is essential in any use of partitioned matrices to represent some matrix product. For example, using [math]A[/math] from equation (6) and [math]B[/math] as: [math]B=\left[\begin{array}{c} B_{11}\\ B_{21}\\ B_{31} \end{array}\right],[/math] it is easy to write:

[math]\begin{aligned} AB & = & \left[\begin{array}{rrr} A_{11} & A_{12} & A_{23}\\ A_{21} & A_{22} & A_{23} \end{array}\right]\left[\begin{array}{c} B_{11}\\ B_{21}\\ B_{31} \end{array}\right]\\ & = & \left[\begin{array}{r} A_{11}B_{11}+A_{12}B_{21}+A_{13}B_{31}\\ A_{21}B_{11}+A_{22}B_{21}+A_{23}B_{31} \end{array}\right].\end{aligned}[/math]

But, what are the row dimensions for the submatrices in [math]B?[/math] What are the possible column dimensions for the submatrices in [math]B?[/math]

Matrices, vectors and econometrics

The data on weights and heights for 12 students in the data matrix: [math]D=\left[\begin{array}{cc} 155 & 70\\ 150 & 63\\ 180 & 72\\ 135 & 60\\ 156 & 66\\ 168 & 70\\ 178 & 74\\ 160 & 65\\ 132 & 62\\ 145 & 67\\ 139 & 65\\ 152 & 68 \end{array}\right][/math] would seem to be ideally suited for fitting a two variable regression model: [math]y_{i}=\alpha+\beta x_{i}+u_{i},\;\;\;\;\; i=1,...,12.[/math] Here, the first column of [math]D[/math] contains all the weight data, the data on the dependent variable [math]y_{i},[/math] and so should be labelled [math]\mathbf{y.}[/math] The second column of [math]D[/math] contains all the data on the explanatory variable height, in the vector [math]\mathbf{x}[/math] say, so that: [math]D=\left[\begin{array}{rr} \mathbf{y} & \mathbf{x}\end{array}\right].[/math]

If we define a [math]12\times1[/math] vector with every element [math]1[/math]: [math]\mathbf{1}_{12}=\left[\begin{array}{c} 1\\ \vdots\\ 1 \end{array}\right],[/math] and a [math]12\times1[/math] vector [math]\mathbf{u}[/math] to contain the error terms; [math]\mathbf{u}=\left[\begin{array}{c} u_{1}\\ \vdots\\ u_{12} \end{array}\right][/math] the regression model can be written in terms of the three data vectors [math]\mathbf{y,1}_{12}[/math] and [math]\mathbf{x}[/math] as: [math]\mathbf{y}=\mathbf{1}_{12}\alpha+\mathbf{x}\beta+\mathbf{u.}[/math] To see this, think of the [math]i[/math]th elements of the vectors on the left and right hand sides.

The standard next step is then to combine the data vectors for the explanatory variables into a matrix: [math]X=\left[\begin{array}{rr} \mathbf{1}_{12} & \mathbf{x}\end{array}\right],[/math] and then define a [math]2\times1[/math] vector [math]\boldsymbol{\delta}[/math] to contain the parameters [math]\alpha,\beta[/math] as: [math]\boldsymbol{\delta}=\left[\begin{array}{r} \alpha\\ \beta \end{array}\right][/math] to give the data matrix representation of the regression model as: [math]\mathbf{y}=X\boldsymbol{\delta}+\mathbf{u.}[/math]

For the purposes of developing the theory of regression, this is the most convenient form of the regression model. It can represent regression models with any number of explanatory variables, and thus any number of parameters. The obvious point is that a knowledge of vector and matrix operations is needed to use and understand this form.

We shall see later that there are two particular matrix and vector quantities associated with a regression model. The first is the matrix [math]X^{T}X,[/math] and the second the vector [math]X^{T}\mathbf{y.}[/math] The following Matlab code snippet provides the numerical values of these quantities for the weight data:

>> dset = load(’weights.mat’); 

>> xtx = dset.X’ * dset.X; 

>> xty = dset.X’ * dset.y; 

>> disp(xtx) 

 12     802

802   53792

>> disp(xty)

  1850

124528

Hand calculation is of course possible, but not recommended.